In this problem set we present four questions:
(Middle School Students)
The irrational number is formed
by using alternating blocks of and zeros, where the
th block
of zeros following the decimal contains zeros. What is the digit
in the 2550th place following the decimal?
(High School Students) Consider the function given by
Find the maximum and minimum value of the function.
(Undergraduate Students) Let be an infinitely differentiable function, such that
-
whenever
-
and
where
and
is the
-th derivative of
Let is given by
Decide whether is infinitely differentiable on
.
(Masters Students and above) If is a measurable subset of
such that
then has measure
Undergraduate : No, it may not be.Consider the function $ $Since
$Since 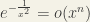 as
as 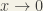 for each
for each  , it can be shown inductively that its k-th derivative
, it can be shown inductively that its k-th derivative 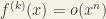 as
as 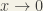 and
and 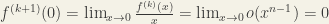 for each
for each 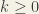 .Hence
.Hence  is a
is a 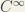 function and satisfies the hypothesis of the question.Now we show that the second derivative of the function
function and satisfies the hypothesis of the question.Now we show that the second derivative of the function 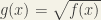 is discontinuous at
is discontinuous at  .For
.For  ,
,  . At
. At  the second term
the second term 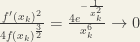 as
as  . But the first term
. But the first term 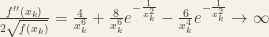 as
as  . Hence
. Hence  as
as  but
but  So
So 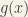 is not a
is not a  function.
function.
On the other hand, the function $
function $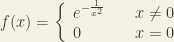 $ is such that
$ is such that  for each
for each  and clearly its square root
and clearly its square root 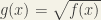 is also a
is also a  function
function
the digit in the 2550th place is 4. The first 71 blocks consist of 2546 digits. the 4th digit of the 72 th block is 4, which is the 2550 digit. we can guess that 2550 th digit occured in the 72 th block by using 5+6+…….+n=2550, which gives n=71.05.
the digit in the 2550th place is 4. The first 71 blocks consist of 2546 digits. the 4th digit of the 72 th block is 4, which is the 2550 digit. we can guess that 2550 th digit occured in the 72 th block by using 5+6+…….+n=2550, which gives n=71.05.
the digit in the 2550th place is 4. The first 71 blocks consist of 2546 digits. the 4th digit of the 72 th block is 4, which is the 2550 digit. we can guess that 2550 th digit occured in the 72 th block by using 5+6+…….+n=2550, which gives n=71.05.
For the undergraduate problem, I guess something surprising is going to happen…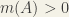 , take a rectangle almost occupied by
, take a rectangle almost occupied by 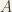 . Choose a point
. Choose a point 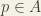 sufficiently close to its center and consider reflection about
sufficiently close to its center and consider reflection about 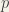 .
.
For the graduate problem, if
For the high school problem, the maximum of should be attained at the solutions of
should be attained at the solutions of  in the interval
in the interval ![[\pi/2, 3\pi/2]](https://s0.wp.com/latex.php?latex=%5B%5Cpi%2F2%2C+3%5Cpi%2F2%5D&bg=f4f2e7&fg=333333&s=0&c=20201002) . Numerically it is
. Numerically it is
 with
with 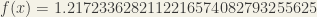 .
.
The value at 4.6 (slightly smaller than 3*pi/2 exceeds the value at 3*pi/2.
Kavi Rama Murthy
I am trying to give solution to the problem for high school students
f(x)=1-(sinx/x) for x not equal to 0
=0 otherwise
as x-sinx>0, 1>sinx/x
therefore 1-sinx/x will be positive for x belongs to (0,pi/2] & as x takes values greater the numerator of sinx/x will be greater hence the 1-sinx/x will be positive
therefore minimum value of f(x)=0
in [pi,3pi/2]
sinx is negative
hence at 3pi/2 the valiue of sinx/x will be -2/(3pi)
hence value of f(x) becomes 1-(-2/(3pi)) i.e. 1+2/3(pi)
as x takes value greater the value of sinx/x will be very very small
hence at x=3pi/2 f(x) is maximum
hence maximum of f(x)=1+2/3(pi)